Accelerazione di Coriolis: la forza “misteriosa” che plasma la dinamica dell’atmosfera
Una spiegazione accompagnata da esperimenti per capire come nasce questa forza e quali effetti curiosi determina

Una delle prime difficoltà in cui si imbatte lo studente che si affaccia alla meteorologia è costituita dall’incontro con l’accelerazione di Coriolis (dal nome del matematico francese che la descrisse nell’Ottocento).
Ben presto, di solito entro la prima decina di pagine del manuale, lo studente scopre che i moti dell’atmosfera, in particolare alle medie e alte latitudini, sono fortemente condizionati dalla rotazione terrestre; approfondendo la materia la meraviglia aumenta perché si impara che la meteorologia delle medie latitudini è legata a una continua ricerca dell’equilibrio: una sorta di balletto, tra le forze dovute ai dislivelli (gradienti) di pressione e l’accelerazione che deriva dalla rotazione del pianeta. La accelerazione di Coriolis è dovuta proprio alla rotazione terrestre.
Forse questa forza ci appare elusiva perché nessuno di noi ha con essa alcuna familiarità: nelle condizioni normali della vita, ha un’intensità trascurabile rispetto alle altre forze con cui abbiamo comunemente a che fare, come ad esempio quella di gravità; inoltre, a differenza dell’accelerazione centrifuga (sua parente stretta), l’accelerazione di Coriolis sembra opporre una resistenza maggiore ad una descrizione intuitiva.
L’esperimento elementare per familiarizzare con l’accelerazione di Coriolis proposto dall’ufficio meteorologico britannico (Metoffice)
Concentriamoci sull’accelerazione di Coriolis e immaginiamo, per semplicità, di osservare un oggetto in moto senza attrito con velocità v sopra a un disco in rotazione antioraria con velocità angolare ω. Il calcolo ci dimostra che nel sistema di riferimento solidale con il disco l’oggetto subisce un’accelerazione verso destra di intensità pari a 2ωv (due omega moltiplicata per la velocità dell’oggetto). Torneremo più avanti (in particolare nel box di approfondimento) sul significato di questa formula. Per il momento, aiutandoci con la figura 1 e con il relativo video proposto dal Metoffice, proviamo a descrivere in modo qualitativo cosa succede. L’oggetto, nel sistema di riferimento “esterno”, non solidale con il disco rotante, si muove lungo una retta (nel video si tratta della punta del pennarello che si sposta lungo il righello); ma nel sistema di riferimento rotante, sul disco, la traiettoria descritta dal suo movimento è giocoforza una curva, e se ci pensiamo bene, si tratta di una curva tanto più stretta quanto più veloce è la rotazione del disco. Se avete compreso questo esperimento (che può essere eseguito anche a livello mentale) avete compreso l’essenza dell’accelerazione di Coriolis. A ben guardare sembra che non sia intervenuta l’azione di alcuna forza , perché la deviazione del moto dell’oggetto è solo l’effetto del diverso sistema di riferimento con cui descriviamo il medesimo moto, ed è per questo motivo che quella di Coriolis viene talora definita una “forza apparente”. Un aggettivo per certi versi fuorviante per noi che passiamo un ‘intera esistenza sopra una sfera rotante osservando ogni giorno l’evoluzione meteorologica che ne è così fortemente influenzata.
| Una spiegazione dell’origine del termine 2ωv
Nella ricerca di una deduzione di carattere euristico dell’accelerazione di Coriolis si finisce di solito per incontrare un esempio basato su un disco rotante con velocità angolare ω, come quello che abbiamo appena incontrato (il disco semplifica la matematica rispetto alla sfera, ma il concetto non cambia). In questo esercizio (con riferimento alla figura a fianco) c’è un punto P in movimento con velocità relativa Vr dalla periferia del cerchio, di raggio r, verso il centro; il disco ruota in senso antiorario (il senso della rotazione terreste se immaginiamo di guardare la Terra da un punto fisso sopra il Polo Nord). Notiamo che il punto P a distanza r dal centro possiede anche una velocità tangenziale periferica pari a ωr, dovuta alla rotazione del disco. Spostandosi verso il centro del disco lungo la traiettoria OP il punto devierà a destra della stessa poiché i punti più interni del disco hanno una velocità tangenziale minore.
|
Esempi e curiosità legati all’accelerazione di Coriolis in ambito non atmosferico
Nella vita di tutti i giorni non è facile accorgersi degli effetti della rotazione terrestre (sarà vero o no che il moto dell’acqua che scende nello scarico del lavandino ne è influenzato?) ed è per questo che sono stati necessari esperimenti relativamente sofisticati per poterli misurare.
L’esperimento forse più famoso è stato eseguito dallo scienziato francese Foucault nel 1851 con il suo pendolo: una palla di cannone appesa a un cavo di ben 67 m, fissato alla cupola del Pantheon di Parigi. Il piano di oscillazione del pendolo ruota in senso orario con un periodo di circa 30 ore proprio a causa dell’accelerazione di Coriolis che, impercettibilmente, devia la palla verso destra durante ogni movimento oscillatorio. Notiamo che se il pendolo si fosse trovato esattamente sopra il Polo Nord, il periodo, concordemente all’intuizione, sarebbe stato pari a quello delle rotazione terrestre, di circa 24 ore.
Alla latitudine di Parigi la forza di Coriolis è invece meno intensa: poiché la Terra è approssimativamente sferica (e non un disco) alla quantità ω bisogna sostituire il prodotto di ω per il seno della latitudine, ovvero la componente del vettore velocità angolare sulla verticale locale, massima al polo, nulla all’equatore. Se invece l’esperimento fosse stato condotto nell’emisfero australe, dove l’accelerazione di Coriolis devia i corpi verso sinistra, la rotazione del piano di oscillazione sarebbe avvenuta in senso opposto.

In generale, un corpo posto in assenza di attrito su un sistema rotante, animato di velocità relativa Vr e in assenza dell’azione di altre forze a causa dell’effetto Coriolis, viene forzato a eseguire un moto circolare definito “cerchio di inerzia” con raggio pari a Vr/2ω e periodo T pari a π/ω dove ancora una volta omega rappresenta la velocità di rotazione del sistema (per convincersene, conoscendo un po’ di matematica, una dimostrazione la si torva nell’introduzione di questo articolo).
In altre parole, come suggerisce il termine “inerzia”, l’accelerazione di Coriolis ha un effetto simile all’azione di una molla che tende a riportare l’oggetto al punto di partenza. Un aspetto interessante è che questi cerchi di inerzia sono stati descritti nel mondo reale, osservando il movimento di alcune boe alla deriva sul mare.
Un esempio a scala più piccola dell’effetto Coriolis è fornito dall’esperimento conosciuto come “le colonne di Taylor”, dal nome del fisico che lo ideò. La prova può essere riprodotta anche fra le mura domestiche. Per svolgerlo si versa dell’acqua in un recipiente che viene mantenuto in uno stato di rotazione abbastanza veloce (ponendolo ad esempio sopra un vecchio giradischi). In queste condizioni, dopo un minimo tempo di assestamento, la superficie dell’acqua assume una forma concava e in ogni punto del fluido si stabilisce un equilibrio tra la forza centrifuga, che tende a spingere il fluido verso l’esterno, e la forza di pressione associata alla gravità che invece attira il fluido verso il centro. E’ possibile dimostrare sia teoricamente che sperimentalmente che in questa situazione, in contrasto con il senso comune, il fluido tende a comportarsi più rigidamente.
Se vengono versate nell’acqua delle gocce di inchiostro si può verificare che l’inchiostro si disperde prevalentemente in senso verticale producendo appunto delle “colonne”. La diluizione nella direzione orizzontale è ostacolata dall’effetto di Coriolis: se la rotazione del recipiente è abbastanza veloce, infatti, una particella di inchiostro che inizia a muoversi in direzione orizzontale è sottoposta alla sua forza e inizia a percorrere cerchi di inerzia di raggio molto piccolo: la particella di acqua con l’inchiostro tende quindi a ritornare al punto di partenza.

Il ruolo dell’accelerazione di Coriolis nella dinamica dell’atmosfera
L’accelerazione di Coriolis influenza profondamente i moti dell’atmosfera sulla scala planetaria e sinottica, cioè alle scale maggiori. Descrivere l’influsso di questa forza, che compare nelle equazioni fondamentali del moto, equivarrebbe quindi a scrivere un trattato di meteorologia. Ci limitiamo pertanto a ricordare che sulla scala sinottica (dove i moti si estendono per lunghezze dell’ordine di 1000 km con velocità dell’ordine di grandezza di 10 m/s) l’accelerazione di Coriolis è comparabile, per intensità, a quella dovuta ai gradienti di pressione.
Il vento geostrofico, un vento definito matematicamente eguagliando la forza di Coriolis con la forza di gradiente, approssima infatti i moti sulla scala sinottica con errore entro il 10%. La parte di vento che non è in equilibrio geostrofico (detta vento ageostrofico) è legata ai moti verticali, alle accelerazioni e, in definitiva, è ciò che rende interessante la meteorologia.
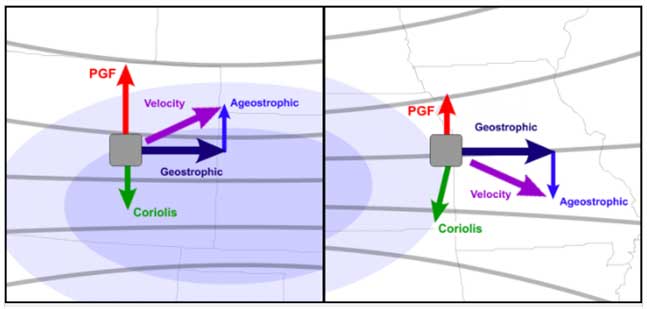
Nella cornice interpretativa in cui è definito il vento geostrofico il flusso evolve nel tempo proprio grazie alla componente ageostrofica diretta perpendicolarmente al vento geostrofico, accelerandolo grazie alla forza di Coriolis. Per pesare l’influsso di questa forza i fisici dell’atmosfera utilizzano una grandezza adimensionale chiamata numero di Rossby, definita dal rapporto fra l’accelerazione del fluido e l’accelerazione di Coriolis: U/fL, dove U e L sono rispettivamente la velocità e la lunghezza tipica del fenomeno che stiamo descrivendo, mentre f=2ωsin(φ) essendo φ la latitudine. Il moti dove l’accelerazione di Coriolis è importante, come quelli sinottici, sono caratterizzati da un numero di Rossby molto minore di 1, mentre grandi numeri di Rossby denotano un flusso dove l’effetto della rotazione terrestre è trascurabile. Sapendo che f alle nostre latitudini è pari a circa a 1/10000 lasciamo volentieri al lettore l’esercizio di stabilire se il moto dell’acqua che scorre nei nostri lavandini è influenzato, come suggerisce una leggenda, dalla rotazione del pianeta.
| Per un approfondimento e per altre curiosità sull’effetto Coriolis si consiglia la lettura di “L’effetto Coriolis – un conflitto tra senso comune e matematica” un articolo di Anders Persson (meteorologo svedese recentemente scomparso), pubblicato su Nimbus (numero 37-38) e scaricabile a questo indirizzo. |
